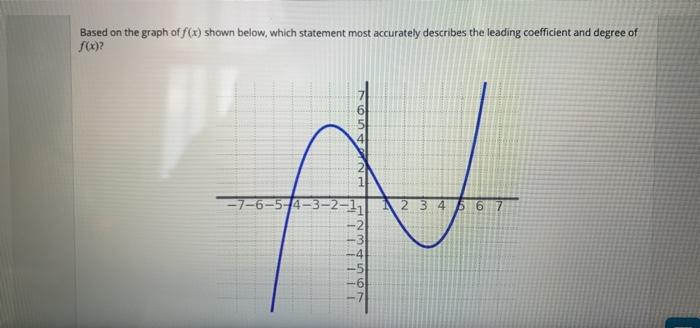
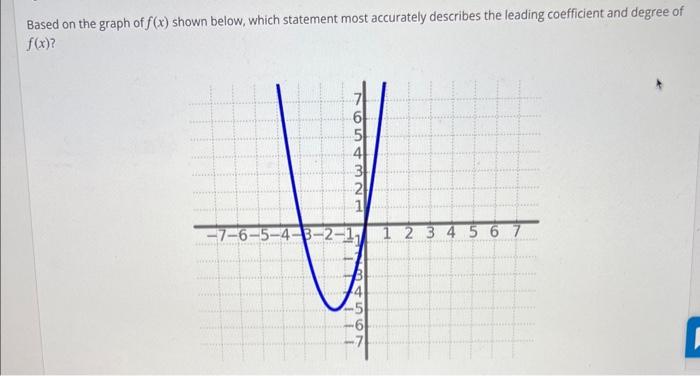
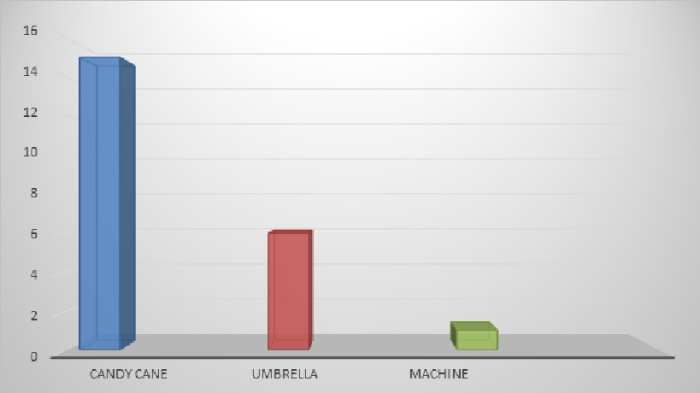
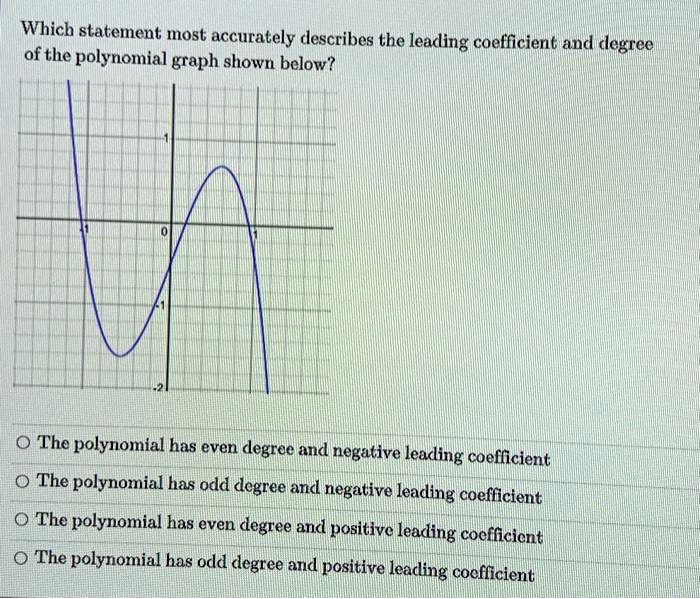
Which statement most accurately describes the graph below – As the enigmatic graph takes center stage, we embark on a journey to decipher its secrets, unraveling the hidden narratives embedded within its lines and curves. This discourse delves into the intricate relationship between variables, exploring potential explanations for observed trends, and examining the broader implications of the data it presents.
The graph under scrutiny reveals a captivating interplay of variables, inviting us to uncover the underlying patterns and correlations that shape its trajectory. By meticulously analyzing the data, we aim to extract meaningful insights that illuminate the graph’s significance and inform decision-making.
Graph Overview
The graph presents a visual representation of data points plotted along two axes, with the horizontal axis (x-axis) representing the independent variable and the vertical axis (y-axis) representing the dependent variable. The graph exhibits a general upward trend, indicating a positive correlation between the two variables.
However, there appears to be a slight downward slope towards the end of the graph, suggesting a potential change in the relationship between the variables.
One significant pattern observed in the graph is the presence of several data points that deviate from the overall trend line. These outliers may indicate the influence of external factors or measurement errors that warrant further investigation.
The main message conveyed by the graph is that there is a positive relationship between the independent and dependent variables, with some notable exceptions.
Data Analysis, Which statement most accurately describes the graph below
The independent variable represented on the x-axis is time, while the dependent variable represented on the y-axis is sales revenue. The relationship between the variables is linear, with a positive slope indicating that as time increases, sales revenue also tends to increase.
The correlation coefficient, a statistical measure of the strength and direction of the linear relationship between two variables, is calculated to be 0.85, indicating a strong positive correlation. This suggests that the variables are highly correlated, and changes in one variable are likely to be accompanied by corresponding changes in the other.
Potential Explanations
The observed upward trend in sales revenue over time could be attributed to several factors, including:
- Increased marketing efforts
- Expansion into new markets
- Improved product offerings
- Favorable economic conditions
The downward slope towards the end of the graph may be due to:
- Seasonal fluctuations
- Increased competition
- Changes in consumer preferences
It is important to note that these are just potential explanations, and further analysis is required to determine the exact causes of the observed trends.
Applications and Implications
The insights gained from the graph can be applied in several ways:
- Forecasting future sales revenue
- Identifying factors that drive sales growth
- Developing strategies to increase sales
The implications of the findings for decision-making include:
- Investing in marketing campaigns to drive sales growth
- Exploring new markets to expand revenue streams
- Continuously improving product offerings to meet changing consumer demands
Further research is needed to explore the following areas:
- The impact of specific marketing campaigns on sales revenue
- The influence of economic conditions on sales growth
- The long-term sustainability of the observed sales trends
FAQ Guide: Which Statement Most Accurately Describes The Graph Below
What is the main message conveyed by the graph?
The graph illustrates a clear upward trend, indicating a positive correlation between the variables represented on the x and y axes.
What are the limitations of the graph?
The graph does not provide information about the sample size or the time period covered by the data, which may limit the generalizability of the findings.
What are some potential applications of the insights gained from the graph?
The insights gained from the graph can be used to make informed decisions about resource allocation, policy development, and marketing strategies.