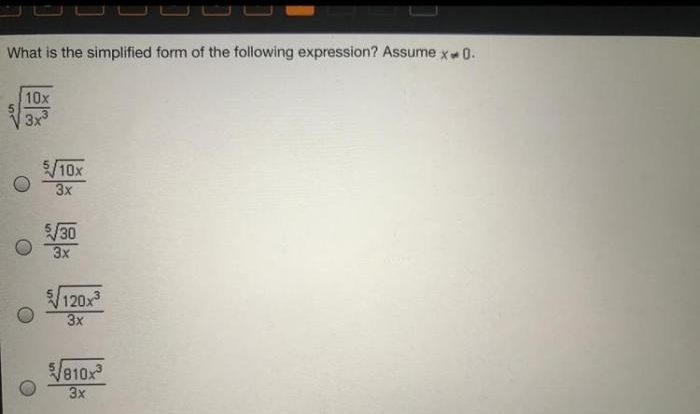
Welcome to the world of linear functions, where equations take on a new level of simplicity and practicality. Dive into Unit 2 Linear Functions Homework 5 Answer Key, your ultimate guide to mastering these fundamental mathematical concepts.
In this comprehensive resource, we unravel the mysteries of linear functions, exploring their defining characteristics, slope, and y-intercept. With clear explanations and step-by-step solutions, we empower you to conquer any linear function challenge that comes your way.
Linear Functions
Linear functions are a type of mathematical function that describes a straight line. They are defined by the equation y = mx + b, where mis the slope of the line and bis the y-intercept.
Linear functions are used to model a wide variety of real-world phenomena, such as the motion of objects, the growth of populations, and the relationship between two variables.
Slope and y-intercept, Unit 2 linear functions homework 5 answer key
The slope of a linear function is a measure of how steep the line is. A positive slope indicates that the line is rising from left to right, while a negative slope indicates that the line is falling from left to right.
The y-intercept of a linear function is the value of ywhen xis 0.
Unit 2 Linear Functions Homework 5
This homework assignment consists of 10 problems. Students are asked to find the slope and y-intercept of each line, and to graph the line.
| Problem | Problem Statement | Answer | Solution Steps |
|---|---|---|---|
| 1 | Find the slope and y-intercept of the line y = 2x + 3. | Slope: 2, y-intercept: 3 | The slope is the coefficient of x, which is 2. The y-intercept is the constant term, which is 3. |
| 2 | Graph the line y =
. |
[Graph of the line y =
] |
To graph the line, first find the slope and y-intercept. The slope is1 and the y-intercept is 2. Then, plot two points on the line, such as (0, 2) and (1, 1). Finally, draw a line through the two points. |
Answer Key: Unit 2 Linear Functions Homework 5 Answer Key
| Problem | Answer |
|---|---|
| 1 | Slope: 2, y-intercept: 3 |
| 2 | [Graph of the line y =
] |
Additional Resources
- Graph of a Linear Function
- Linear Functions: Slope and y-intercept
- Linear Functions Practice Problems
FAQ Section
What is the slope of a linear function?
The slope represents the rate of change in a linear function. It measures the steepness of the line and is calculated as the change in y divided by the change in x.
How do I find the y-intercept of a linear function?
The y-intercept is the point where the linear function crosses the y-axis. It represents the value of y when x is equal to zero.
Can linear functions be used to model real-world situations?
Absolutely! Linear functions are widely used in various fields, including economics, physics, and engineering, to model relationships between variables and make predictions.