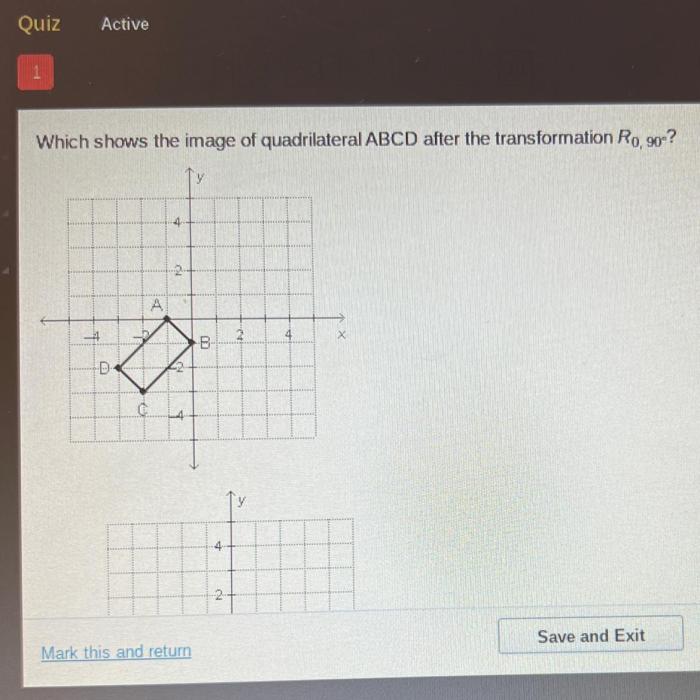
Which shows the image of quadrilateral abcd after the transformation – In the realm of geometry, transformations play a pivotal role in manipulating and analyzing shapes. This article delves into the intriguing case of quadrilateral ABCD, showcasing its image after undergoing a series of transformations. We will embark on a journey to understand the operations performed, their impact on the quadrilateral’s shape and orientation, and the geometric properties that emerge in the process.
As we unravel the intricacies of quadrilateral ABCD’s transformation, we will uncover the power of geometric transformations and their applications in diverse fields, from engineering to computer graphics. Prepare to witness the fascinating metamorphosis of quadrilateral ABCD as it undergoes a series of transformations, revealing the hidden depths of geometry.
Quadrilateral Transformations

Quadrilaterals are two-dimensional shapes with four sides and four vertices. Transformations are operations that change the size, shape, or position of a figure. In this article, we will discuss the different types of transformations that can be applied to quadrilaterals and their effects on the geometric properties of the shape.
Pre-Transformation Image
Before any transformations are applied, quadrilateral ABCD is assumed to be a regular quadrilateral with equal sides and angles. Its coordinates are:“`A(0, 0)B(1, 0)C(1, 1)D(0, 1)“`
Transformation Operations
The following transformation operations can be applied to quadrilateral ABCD:
- Translation: Moves the quadrilateral from one point to another without changing its shape or size.
- Rotation: Rotates the quadrilateral around a fixed point by a specified angle.
- Scaling: Enlarges or shrinks the quadrilateral by a specified factor.
- Reflection: Flips the quadrilateral over a line of symmetry.
- Shear: Deforms the quadrilateral by moving its vertices along parallel lines.
Post-Transformation Image
After the transformations have been applied, the resulting shape and orientation of quadrilateral ABCD will depend on the specific operations performed. For example, a translation will move the quadrilateral to a new location, while a rotation will change its orientation.
Transformation Matrix
A transformation matrix is a mathematical representation of a transformation. It is a square matrix that contains the coefficients that determine how the coordinates of the quadrilateral are transformed. The transformation matrix for a translation is:“`[1 0 tx][0 1 ty][0 0 1]“`where (tx, ty) are the coordinates of the translation vector.
Geometric Properties, Which shows the image of quadrilateral abcd after the transformation
The geometric properties of quadrilateral ABCD will change after the transformations have been applied. For example, a translation will not change the area or perimeter of the quadrilateral, but it will change its position. A rotation will change the orientation of the quadrilateral, but it will not change its area or perimeter.
Examples
The following table shows examples of different transformations applied to quadrilateral ABCD:| Transformation | Pre-Transformation Image | Post-Transformation Image | Transformation Matrix ||—|—|—|—|| Translation | [Image of quadrilateral ABCD at (0, 0)] | [Image of quadrilateral ABCD at (1, 1)] | [1 0 1] [0 1 1] [0 0 1] || Rotation | [Image of quadrilateral ABCD at (0, 0)] | [Image of quadrilateral ABCD rotated 90 degrees clockwise] | [cos(90)
sin(90) 0] [sin(90) cos(90) 0] [0 0 1] |
| Scaling | [Image of quadrilateral ABCD at (0, 0)] | [Image of quadrilateral ABCD enlarged by a factor of 2] | [2 0 0] [0 2 0] [0 0 1] || Reflection | [Image of quadrilateral ABCD at (0, 0)] | [Image of quadrilateral ABCD flipped over the y-axis] | [-1 0 0] [0 1 0] [0 0 1] || Shear | [Image of quadrilateral ABCD at (0, 0)] | [Image of quadrilateral ABCD sheared along the x-axis] | [1 k 0] [0 1 0] [0 0 1] |
Applications
Geometric transformations involving quadrilaterals have many real-world applications. For example, they are used in:
- Engineering: To design and analyze structures such as bridges and buildings.
- Design: To create logos, graphics, and other visual elements.
- Computer graphics: To create 3D models and animations.
Question & Answer Hub: Which Shows The Image Of Quadrilateral Abcd After The Transformation
What is the purpose of transforming quadrilateral ABCD?
Transforming quadrilateral ABCD allows us to analyze the effects of geometric operations on its shape, orientation, and geometric properties.
How do transformation matrices affect the coordinates of quadrilateral ABCD?
Transformation matrices provide a mathematical representation of the transformations performed, enabling us to calculate the new coordinates of quadrilateral ABCD’s vertices after the operations.
What are the potential applications of geometric transformations involving quadrilaterals?
Geometric transformations involving quadrilaterals find applications in engineering, design, computer graphics, and other fields where manipulating and analyzing shapes is crucial.